FinalFAC

Guión del video final

Tema: IEEE 754 - Historia y funcionamiento

Secciones

  1. Introducción
  2. Historia
  3. Problemas que resulve
  4. ¿Como se compone un numero en IEEE754?
  5. Pasaje de un numero decimal al estandar
  6. Pasaje del estandar a decimal

Introducción

Historia

¿Qué es IEEE?

El Institute of Electrical and Electronics Engineers (IEEE) es una organización profesional internacional dedicada al desarrollo y promoción de estándares técnicos en múltiples áreas de la ingeniería y la tecnología. Fundada en 1963, IEEE agrupa a ingenieros, científicos y profesionales para fomentar la innovación y el avance tecnológico.

El estandar IEEE754

Uno de los roles más importantes que cumplió IEEE es la estandarización de formatos y protocolos. En particular, IEEE fue fundamental en la creación del estándar IEEE 754, publicado en 1985. Este estandar define el formato y las reglas para la representación y manipulación de números en punto flotante en las computadoras.

Gracias a IEEE, el estándar IEEE 754 se convirtió en la base para la mayoría de los procesadores y lenguajes de programación modernos, asegurando resultados consistentes y fiables en cálculos científicos y financieros.

Problemas que resulve

Problemas que resuelve

El estándar IEEE 754 fue creado para resolver varios problemas importantes que surgían al representar números decimales en las computadoras usando formatos binarios y aritmética de punto flotante:

  1. Inconsistencia en la representación de números reales: Antes de IEEE 754, no existía un estándar unificado, por lo que distintos procesadores y lenguajes de programación usaban formatos propios para almacenar números en punto flotante. Esto provocaba resultados diferentes al realizar cálculos idénticos en distintas máquinas o programas.

  2. Falta de precisión y errores acumulativos: Los cálculos con números en punto flotante suelen tener errores por redondeo. IEEE 754 define reglas claras para redondeos, manejo de excepciones y representación de números especiales, minimizando errores y mejorando la precisión en operaciones sucesivas.

  3. Representación de valores especiales: El estándar permite codificar valores como cero positivo y negativo, infinitos (positivo y negativo) y el valor especial NaN (Not a Number), que representan resultados indefinidos o errores en cálculos, facilitando el manejo de casos excepcionales en software y hardware.

  4. Diferentes rangos y precisión para distintas aplicaciones: Al definir formatos de simple y doble precisión (y otros), IEEE 754 ofrece flexibilidad para distintos niveles de precisión y rango de números, optimizando el uso de memoria según la necesidad del cálculo.

  5. Facilitar la portabilidad y consistencia de resultados: Gracias a la estandarización, programas escritos para un sistema pueden funcionar en otro sin cambios en el resultado de cálculos numéricos, haciendo posible el desarrollo de software confiable y portable.

  6. Mejora en performance: Al estandarizar la representación y las operaciones en hardware específico para punto flotante, se consigue una mejora significativa en la velocidad y eficiencia de los cálculos comparado con interpretarlos mediante software, lo que es fundamental para aplicaciones que requieren procesamiento rápido y masivo de datos numéricos de punto flotante.

¿Como se compone un numero en IEEE754?

Un numero en IEEE754 se compone de 3 partes: El bit de signo (1 bit), el exponente (8 bits en simple precision, 11 bits en doble precision), y la mantisa (23 bits en simple precision, 52 bits en doble precision).

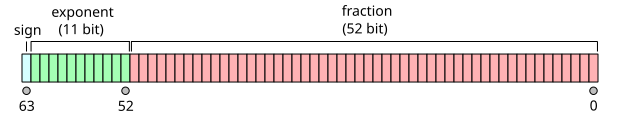
Bit de signo

El bit de signo es la parte que nos indica si el numero tiene que ser interpretado como positivo o negativo. Si es 0, es positivo. Si es 1, es negativo.

Exponentes

Los exponentes se encuentran sesgados por un exceso de $2^{(n-1)} - 1$, donde n es la cantidad de bits del exponente. Como vimos, esto varia dependiendo del formato que se este usando: simple o doble precision.

Exponente en simple precisión

Los exponentes en simple precisión estan representados en un exceso de $2^{(8-1)} - 1 = 2^{(7)} - 1 = 127$. De esta manera, si estamos en el proceso de pasar un decimal a IEEE 754 de precision simple, el exponente real que calculamos al normalizarlo debemos aumentarlo en 127 unidades decimales.

Exponente en doble precisión

Los exponentes en doble precision, calculados con la formula presentada anteriormente estan en un exceso de $2^{(11-1)} - 1 = 2^{(10)} - 1 = 1023 $.

Fraccion o mantisa

La parte de la mantisa se encuentra codificada en binario sin signo, por lo que no recibe alteraciones cuando se cambia de formato (Simple <–> Doble).

Pasaje de decimal al estandar

El pasaje de un numero del sistema decimal al estandar IEEE754 se puede hacer siguiendo distintos pasos. En terminos generales, se debe:

Pasaje del estandar a decimal

El pasaje de un numero expresado mediante el estandar IEEE754 se realiza con los siguientes pasos:

La siguiente formula nos ayuda a visualizar como se interpreta un numero decimal codificado con el estandar IEEE754:

\begin{equation} (-1)^s\times (1,m) \times 2^{e} \end{equation}

donde:

Ejemplos practicos de pasaje entre sistemas

Decimal a IEEE754

1) Pasar 12,375 al estandar.

2) Pasar 5,75 al estandar.

Fuentes / Software utilizado:

This site is open source. Improve this page.